1. Técnicas de conteo
Son una serie de métodos de probabilidad para contar el número posible de arreglos dentro de un conjunto o varios conjuntos de objetos. Estas técnicas son varias, pero las más importantes se dividen en dos principios básicos, que son el multiplicativo y el aditivo; las permutaciones y las combinaciones.
Por ejemplo, es muy sencillo la solución a este problema: imagínate que tu jefe te pide que cuentes los últimos productos que han llegado en la última hora. En este caso podrías ir y contar uno a uno los productos.
Sin embargo, imagina que el problema es este: tu jefe te pide que cuentes cuántos grupos de 5 productos del mismo tipo pueden formarse con los que han llegado la última hora. En este caso, el cálculo se complica. Para este tipo de situaciones se utilizan las llamadas técnicas de conteo.
1.2 Principio aditivo
El principio aditivo es una técnica de conteo en probabilidad que permite medir de cuántas maneras se puede realizar una actividad que, a su vez, tiene varias alternativas para ser realizada, de las cuales se puede elegir solo una a la vez. Un ejemplo clásico de esto es cuando se quiere escoger una línea de transporte para ir de un lugar a otro.
El principio aditivo nos dice que la cantidad de maneras que tenemos para realizar este viaje corresponderá a la suma de cada alternativa (medio de transporte) posible que exista para ir al lugar deseado, esto incluirá aun los medios de transporte que hagan escala en algún lugar (o lugares) intermedio.
Fórmula: P(A∪B)= P(A)+ P(B).
Ejemplo: Si una librería vende libros de literatura, biología, medicina, arquitectura y química, de los cuales posee 15 tipos diferentes de libros de literatura, 25 de biología, 12 de medicina, 8 de arquitectura y 10 de química, ¿Cuántas opciones tiene una persona para escoger un libro de arquitectura o un libro de biología?.
El principio aditivo nos dice que es: 8+25=33.
Es una técnica que se utiliza para resolver problemas de conteo para hallar la solución sin que sea necesario enumerar sus elementos. Es conocido también como el principio fundamental del análisis combinatorio; se basa en la multiplicación sucesiva para determinar la forma en la que puede ocurrir un evento.
Este principio establece que, si una decisión (d1) puede ser tomada de n maneras y otra decisión (d2) puede tomarse de m maneras, el número total de maneras en las que pueden ser tomadas las decisiones d1 y d2 será igual a multiplicar de n * m
Fórmula: N1 * N2… * Nx maneras.
Ejemplo: ¿de cuántas formas se puede vestir una persona que tiene 3 pantalones y 3 camisas?.
Para vestirse, la persona se pone el pantalón y luego la camisa, es decir tiene 3 x 3 = 9 opciones diferentes de vestirse.
¡La función factorial es una fórmula matemática representada por el signo de exclamación “!". En la fórmula Factorial se deben multiplicar todos los números enteros y positivos que hay entre el número que aparece en la fórmula y el número 1.
Fórmula: n! =n (n-1)*(n-2)*(n-3)......(n-i)
¡La función factorial es una fórmula matemática representada por el signo de exclamación “!". En la fórmula Factorial se deben multiplicar todos los números enteros y positivos que hay entre el número que aparece en la fórmula y el número 1.
Fórmula: n! =n (n-1)*(n-2)*(n-3)......(n-i)
Son eventos de tipo multiplicativo, donde el número de posibilidades va disminuyendo y si importa el orden una permutación es un arreglo de un conjunto de objetos en un orden definido. El número de permutaciones diferentes de estos objetos es; esto se ve fácilmente si pensamos que para la primera alternativa disponemos de los elementos del conjunto, cada uno de los cuales puede complementarse con los restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto.
Fórmula de permutaciones sin repetición:
Fórmula de permutaciones con repetición:
Fórmula de permutaciones circulares:
Ejemplo de permutaciones sin repetición: ¿De cuantas formas diferentes se pueden ordenar las letras de la palabra "Auto"?
Tenemos 4 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 4 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada, nos quedan 3 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 2 y así sucesivamente.
El resultado es: 4 x 3 x 2 x 1 = 24
Ejemplo de permutaciones con repetición: ¿Cuántas palabras diferentes podemos formar con las letras de la palabra "Coco"?
Para resolverlo necesitamos analizar lo siguiente:
1.- Veces que aparece la letra "c": 2
2.- Veces que aparece la letra "o": 2
3.- Número de elementos: 4
El resultado es:
El resultado es:
La combinación o combinatoria es una técnica de conteo que se aplica en experimentos aleatorios, en los que no se tiene en cuenta el orden en que se eligen los elementos y no es posible la repetición.
Fórmula:
En este experimento el orden no se tiene en cuenta ya que da el mismo resultado combinar el color amarillo, el verde y el rojo, que, si se toma primero el verde, luego el rojo y por último el amarillo. Con esto, el número de elementos del espacio muestral es:
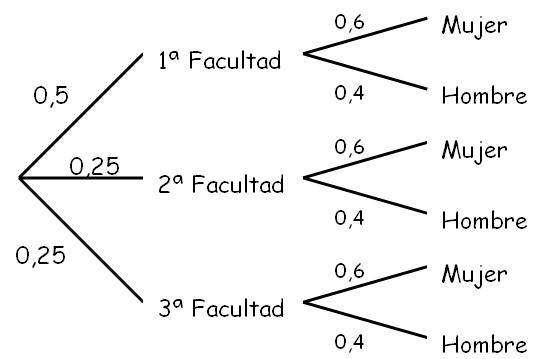
Es una herramienta de calidad que a través de un proceso sistemático nos permite hallar la relación existente entre un concepto general y los elementos que lo componen.
Dicho de otra forma, la herramienta se basa en la visión en conjunto de los medios requeridos (las ramas del árbol) para resolver un problema o alcanzar un objetivo (el tronco del árbol).
Parte de un elemento central (tronco) que se desagrega en otros subelementos más pequeños (ramas de primer nivel), que a su vez también se desagregan en otros elementos; de ahí el nombre de árbol. Así pues, en la medida en que vamos desagregando el elemento central encontramos medios más detallados y accionables.
Es decir, que entre más conseguimos profundizar, el diagrama entrega mayor precisión sobre los medios que deben ser empleados para alcanzar el elemento central "el tronco" por lo que podríamos considerar los niveles superiores como productos u objetivos secundarios.
Representación:








Comentarios
Publicar un comentario